Matemaattisen tarkkaa kaaosta
-----------------------------
Petri Keckman
Luulisi, ettei mikään ole niin tarkkaa kuin matemaattinen tarkkuus, mutta jon-
kinlainen kaaos voi tulla vastaan lukujenkin maailmassa. Osaltaan tämä johtuu
siitä, että tietokoneella voidaan laskea vain äärellisellä tarkkuudella varsin-
kin systeemeissä, jotka ovat hyvin herkkiä alkuarvojen suhteen. Tällaisia ovat
monet luonnontieteen matemaattiset mallit, joissa lasketaan planeettojen ratoja
tai säätä. Kyllä, planeettojenkin liikkeissä on samanlaisia pienestä sattumasta
kiinni olevia heilahteluja kuin sääilmiöissä. Viimeksi mainituista yksi tunne-
tuimmista on perhosefekti: jos jotakin perhosen siiven iskua ei olisi viime
vuonna tapahtunut, niin jokin hirmumyrsky olisi vältetty tänä vuonna tai toi-
sinpäin. Vuosituhansien saatossa saattavat pienet ja kaukaiset tekijät vaikuttaa
planeettojen kiertoratoihinkin. Kun tähän lisätään vielä kvanttimekaniikan tuoma
sattumallisuus mikromaailman ilmiöihin, niin ainakaan niitä ei voida ennustaa.
Tietokoneella on helppo tutkia numeerisesti sellaisia käsitteitä kuin jaksolli-
suus, kaaos ja tasapainotila. Esimerkiksi hyvin yksinkertainen rekursiivinen
kaava x:=1-q*x*x, missä x:lle lasketaan arvo x:n edellisen arvon perusteella.
Valitaan q väliltä nollasta kahteen. Jos q on nolla, niin sarja saa heti arvon
yksi ja pysyy siinä, sillä 1=1-0*x*x, vaikka x olisi mikä tahansa luku. Tutki-
taan E-kielisellä ohjelmalla, miten käy kun q=0.1. On selvää, että jos sarja saa
missä tahansa vaiheessa saman arvon kuin joskus aikaisemmin, niin se ei kehity
vaan toistaa itseään. Seuraavassa ohjelman pätkässä lasketaan kymmenen lukua
kerralla taulukkoon ja tutkitaan, onko niiden joukossa samoja. E-kielessä ovat
desimaaliluvut aivan tavallisia LONG-tyyppisiä 32-bittisiä (kokonais)lukuja,
joille vain on omat laskutoimitukset. Muuttujan ja laskutoimituksen tulkitsemi-
nen reaalityyppiseksi merkitään huutomerkillä, samoin muunnokset lukutyyppien
välillä. Lukuarvo tulkitaan desimaaliluvuksi (tai float, real - mikä se onkaan),
jos siinä on desimaalipiste.
PROC main()
DEF x[10]: ARRAY OF LONG,
s[20]:STRING, /* apumuuttuja reaalilukujen tulostukseen */
x0=0.0, /* alkuarvo Huom! desimaalipiste on oltava nollassakin*/
ind=0, /* sarjan alkion indeksi (tämä on 16-bit kokonaisluku) */
i, j, /* taulukkojen käsittelyyn */
q=0.1, /* samoin tässä on oltava "." (vaikka arvo olisi 1.0) */
samoja, /* totuusarvo samojen löytymiselle 10 joukosta */
pot=10 /* apumuuttuja tulostuksen hallintaan */
WriteF('Rekursiokaava x:=1-qxx, missä x[0]=\s ',RealF(s,!x0,8))
WriteF('ja q=\s\n',RealF(s,!q,8))
REPEAT
FOR i:=0 TO 9 /* lasketaan kymmenen kerralla */
x[i]:=!1.0-(!q*x0*x0)
x0:=x[i]
INC ind
ENDFOR
i:=0 /* tarkastetaan löytyikö niiden joukosta */
REPEAT /* samoja */
j:=i+1
REPEAT
samoja:=(!x[i]=x[j])
INC j
UNTIL (j=9) OR samoja
INC i
UNTIL (i=8) OR samoja
/* tulostetaan jos samoja löytyi tai */
/* ind-10 on jaollinen 10
ot:lla */
IF samoja OR (Mod(ind-10,pot)=0)
FOR i:=0 TO 9
WriteF('x[\d] = \s\n',ind+i-9,RealF(s,x[i],8))
ENDFOR
pot:=10*pot
ENDIF
x0:=x[9] /* asetetaan uusi x0 ja jos ei paineta hiirtä, niin */
UNTIL (ind>650000) OR samoja OR (Mouse()=1) /* toistetaan kunnes...*/
WriteF('Ohjelma päättyi.')
ENDPROC
Tuloste:
Rekursiokaava x:=1-qxx, missä x[0]=0.00000000 ja q=0.10000001
x[1] = 1.0
x[2] = 0.90000000
x[3] = 0.91900000
x[4] = 0.91554392
x[5] = 0.91617792
x[6] = 0.91606184
x[7] = 0.91608312
x[8] = 0.91607920
x[9] = 0.91607984
x[10] = 0.91607976
x[11] = 0.91607976
x[12] = 0.91607976
x[13] = 0.91607976
x[14] = 0.91607976
x[15] = 0.91607976
x[16] = 0.91607976
x[17] = 0.91607976
x[18] = 0.91607976
x[19] = 0.91607976
x[20] = 0.91607976
Ohjelma päättyi.
Eli sarja lähestyy hyvin nopeasti arvoa 0.91607976.
Voidaan todeta, ettei raja-arvo (tässä tapauksessa kun q=0.1) riipu sarjan
ensimmäisestä jäsenestä x[0], vaan esim. jos lähdemme arvosta x[0]=-5.0,
niin saamme saman raja-arvon:
Rekursiokaava x:=1-qxx, missä x[0]=-5.0 ja q=0.10000001
x[1] = -1.50000000
x[2] = 0.77500000
x[3] = 0.93993744
x[4] = 0.91165176
x[5] = 0.91688912
x[6] = 0.91593144
x[7] = 0.91610696
x[8] = 0.91607480
x[9] = 0.91608072
x[10] = 0.91607960
x[11] = 0.91607984
x[12] = 0.91607976
x[13] = 0.91607976
x[14] = 0.91607976
x[15] = 0.91607976
x[16] = 0.91607976
x[17] = 0.91607976
x[18] = 0.91607976
x[19] = 0.91607976
x[20] = 0.91607976
Ohjelma päättyi.
Näin käy ainakin niin kauan kuin x[0] ei ole pienempi kuin noin -10.916.
Alkuarvosta -10.917 raja-arvoksi yhtäkkiä tulee 0 (en tiedä miksi). Mutta
annetaan nyt x[0]:n olla aluksi nolla ja tutkitaan raja-arvon määräytymistä
pelkästään q:sta. Olkoon esim. q=0.7:
Rekursiokaava x:=1-qxx, missä x[0]=0.00000000 ja q=0.70000000
x[1] = 1.0
x[2] = 0.30000002
x[3] = 0.93700000
x[4] = 0.38542168
x[5] = 0.89601512
x[6] = 0.43800984
x[7] = 0.86570320
x[8] = 0.47539060
x[9] = 0.84180264
x[10] = 0.50395780
x[101] = 0.67937728
x[102] = 0.67691248
x[103] = 0.67925264
x[104] = 0.67703112
x[105] = 0.67914024
x[106] = 0.67713800
x[107] = 0.67903888
x[108] = 0.67723432
x[109] = 0.67894760
x[110] = 0.67732112
x[261] = 0.67811376
x[262] = 0.67811320
x[263] = 0.67811368
x[264] = 0.67811328
x[265] = 0.67811360
x[266] = 0.67811336
x[267] = 0.67811360
x[268] = 0.67811336
x[269] = 0.67811360
x[270] = 0.67811336
Ohjelma päättyi.
Huomataan, että sarja näyttää kyllä lähestyvän jotain raja-arvoa, mutta ei
tarkasti saavuta sitä, vaan parilliset ja parittomat jäsenet saavuttavat
omansa (vaikkakin hyvin läheiset). Kasvatetaan vielä hieman q:ta: q=0.74:
Rekursiokaava x:=1-qxx, missä x[0]=0.00000000 ja q=0.74000000
x[1] = 1.0
x[2] = 0.26000000
x[3] = 0.94997600
x[4] = 0.33218372
x[5] = 0.91834400
x[6] = 0.37591684
x[7] = 0.89542800
x[8] = 0.40667444
x[9] = 0.87761576
x[10] = 0.43004508
x[1121] = 0.66890328
x[1122] = 0.66890060
x[1123] = 0.66890324
x[1124] = 0.66890060
x[1125] = 0.66890324
x[1126] = 0.66890060
x[1127] = 0.66890324
x[1128] = 0.66890060
x[1129] = 0.66890324
x[1130] = 0.66890060
Edelleen parittomat ja parilliset jäsenet saavuttavat raja-arvonsa erikseen,
mutta nyt hieman myöhemmin. Itse asiassa sarjan pitäisi saavuttaa
yksikäsitteinen raja-arvo, jota ei tietokoneella saavuteta. Raja-arvo on
helppo laskea: onhan se kiintopiste eli piste, jossa x=1-q*x*x, jolla on
toisen asteen yhtälön (q*x*x+x-1=0) ratkaisu, kun x=(-1+-Sqrt(1+4q))/(2*q)
eli edellisellä sarjalla olisi pitänyt olla raja-arvo:
(-1+Sqrt(1+4*0.74))/(2*0.74)=0.668901942...
Tutkitaan vielä arvoa q=0.75:
Rekursiokaava x:=1-qxx, missä x[0]=0.00000000 ja q=0.75000000
x[1] = 1.0
x[2] = 0.25000000
x[3] = 0.95312504
x[4] = 0.31866456
x[5] = 0.92383968
x[6] = 0.35989016
x[7] = 0.90285928
x[8] = 0.38863384
x[9] = 0.88672280
x[10] = 0.41029204
x[101] = 0.75357712
x[102] = 0.57409112
x[103] = 0.75281456
x[104] = 0.57495272
x[105] = 0.75207200
x[106] = 0.57579076
x[107] = 0.75134872
x[108] = 0.57660628
x[109] = 0.75064392
x[110] = 0.57740028
x[1001] = 0.69596128
x[1002] = 0.63672840
x[1003] = 0.69593272
x[1004] = 0.63675828
x[1005] = 0.69590416
x[1006] = 0.63678800 Tietokoneella on helppo tehdä monisivuisia
x[1007] = 0.69587576 numeroita käsitteleviä artikkeleita.
x[1008] = 0.63681764
x[1009] = 0.69584744
x[1010] = 0.63684724
x[10001] = 0.67605248
x[10002] = 0.65721476
x[10003] = 0.67605152
x[10004] = 0.65721572
x[10005] = 0.67605064
x[10006] = 0.65721668
x[10007] = 0.67604968
x[10008] = 0.65721764
x[10009] = 0.67604872
x[10010] = 0.65721852
x[52601] = 0.67077388
x[52602] = 0.66254676
x[52603] = 0.67077388
x[52604] = 0.66254676
x[52605] = 0.67077388
x[52606] = 0.66254676
x[52607] = 0.67077388
x[52608] = 0.66254676
x[52609] = 0.67077388
x[52610] = 0.66254676
Ohjelma päättyi.
Kestää yhä kauemmin, ennen kuin sarja saavuttaa raja-arvonsa. Itse asiassa
0.75 on "katastrofipiste", jonka jälkeen sarjan ei matemaattisestikaan
pitäisi saavuttaa yksikäsitteistä raja-arvoa vaan kaksi erillistä. Esim.
q=0.76:
Rekursiokaava x:=1-qxx, missä x[0]=0.00000000 ja q=0.76000000
x[1] = 1.0
x[2] = 0.24000000
x[3] = 0.95622400
x[4] = 0.30508310
x[5] = 0.92926248
x[6] = 0.34371816
x[7] = 0.91021192
jne..., kunnes sarja saavuttaa melko nopeasti kaksi raja-arvoansa:
x[511] = 0.78947528
x[512] = 0.52631384
x[513] = 0.78947528
x[514] = 0.52631384
x[515] = 0.78947528
x[516] = 0.52631384
x[517] = 0.78947528
x[518] = 0.52631384
x[519] = 0.78947528
x[520] = 0.52631384
Ohjelma päättyi.
q:n arvolla 1 sarja saavuttaa heti kaksi raja-arvoaan: 0 ja 1:
1-1*0*0=1 ja 1-1*1*1=0.
Mutta saavuttaako se ne kaikilla x[0]:n lähtöarvoilla?
Rekursiokaava x:=1-qxx, missä x[0] = 0.12300001 ja q=1.0
x[1] = 0.98487096
x[2] = 0.03002918
x[3] = 0.99909824
x[4] = 0.00180268
x[5] = 0.99999672
x[6] = 0.00000656
x[7] = 1.0
x[8] = 0.00000000
x[9] = 1.0
x[10] = 0.00000000
Ohjelma päättyi.
Saavuttaa, ja melko nopeasti. Paitsi: on olemassa arvo x[0]=0.618033988,
joka on kiintopiste:
Rekursiokaava x:=1-qxx, missä x[0]=0.61803400 ja q=1.0
x[1] = 0.61803396
x[2] = 0.61803400
x[3] = 0.61803396
x[10001] = 0.61803396
x[10002] = 0.61803400
x[10003] = 0.61803396
x[10004] = 0.61803400
x[10005] = 0.61803396
x[10006] = 0.61803400
x[10007] = 0.61803396
x[10008] = 0.61803400
x[10009] = 0.61803396
x[10010] = 0.61803400
Sarja on ja pysyy siinä, mutta jos siihen tehdään pieni poikkeama - eli
perhosen siivenisku tai hyttysen aivastus häiritsemässä Jupiterin
kiertorataa - niin:
Rekursiokaava x:=1-qxx, missä x[0]=0.61803300 ja q=1.0
x[1] = 0.61803520
x[2] = 0.61803244
x[3] = 0.61803584
x[4] = 0.61803168
x[5] = 0.61803680
x[6] = 0.61803048
x[7] = 0.61803828
x[8] = 0.61802864
x[9] = 0.61804056
x[10] = 0.61802584
x[101] = 1.0
x[102] = 0.00000000
x[103] = 1.0
x[104] = 0.00000000
Sarja saavuttaa kaksi raja-arvonsa 1 ja 0 taas melko nopeasti.
Jatketaan q:n kasvattamista (ja annetaan x[0]:n olla taas aina 0). Seuraava
katastrofipiste on q=1.25, jossa sarja ei saavuta kahta, vaan neljä
raja-arvoansa:
Rekursiokaava x:=1-qxx, missä x[0]=0.10000001 ja q=1.25000000
x[1] = 0.98750000
x[2] = -0.21894538
x[3] = 0.94007864
x[4] = -0.10468484
x[5] = 0.98630136
x[6] = -0.21598792
jne..., jolloin sarja saavuttaa (tietokoneella kahdeksan desimaalin
tarkkuudella) neljä raja-arvonsa, mutta ei kovin nopeasti:
x[17121] = 0.96672512
x[17122] = -0.16819692
x[17123] = 0.96463720
x[17124] = -0.16315615
x[17125] = 0.96672512
x[17126] = -0.16819692
x[17127] = 0.96463720
x[17128] = -0.16315615
x[17129] = 0.96672512
x[17130] = -0.16819692
Ohjelma päättyi.
Kun q:ta kasvatetaan ja annetaan sen lähestyä 1.401:tä, niin huomataan, että
tällä välillä raja-arvojen määrä kaksinkertaistuu yhä uudestaan ja uudestaan,
niin että mitä lähempänä 1.401:tä q on, sitä useampia raja-arvoja se saavuttaa.
Kaikesta edellä mainitusta voidaan ohjelmalla aikaansaada kuva:
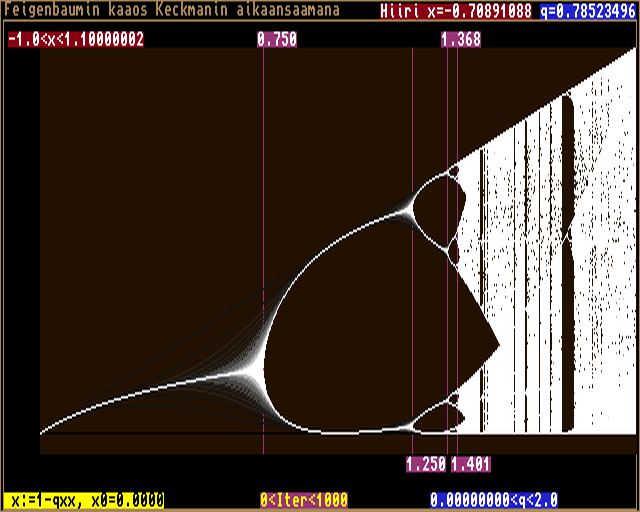
kuva 1:
Siinä siis q kasvaa vasemmalta oikealle 0 < q< 2 ja x kasvaa ylhäältä alas -1 < x < 1.1. Sarjan ensimmäiset arvot (0 ja 1 jne.) plotataan mustilla pis- teillä ja sitä valkoisemmilla, mitä suurempi järjestysnumero niillä on. Sel- keästi nähdään ne pisteet, joissa raja-arvot kahdentuvat. Kuvasta nähdään, kuin- ka pisteessä q=0.75 sarja saavuttaa raja-arvon. Mutta jos zoomataan aluetta, niin havaitaan, että se on harhaa: kuva 2 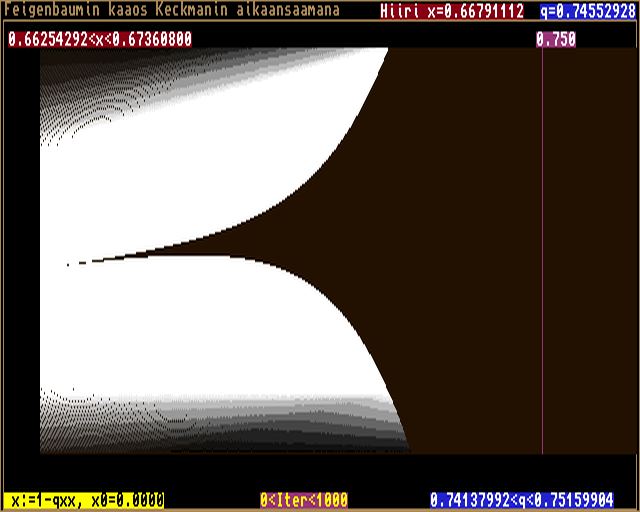
Kuvasta 2 nähdään selvästi ("perseen muodossa"), kuinka sarja ei todellisuudessa
koskaan saavuta raja-arvoa pisteessä q=0.75 (vaikka äärellisen laskutarkkuuden
omaavalla tietokoneella sen myös numeerisesti edellä saavuttikin).
Kuvasta 1 nähdään myös, kuinka pisteen q=1.401 jälkeen sarja ei saavuta yleensä
mitään raja-arvoja, vaan heilahtelee summittaisesti(?) - mutta matemaattisen
tarkasti - tiettyjen arvojen välillä. Kuitenkin tämänkin pisteen jälkeen on ha-
vaittavissa alue (q>1.75), jossa sarja saavuttaa kolme tarkkaa raja-arvoa:
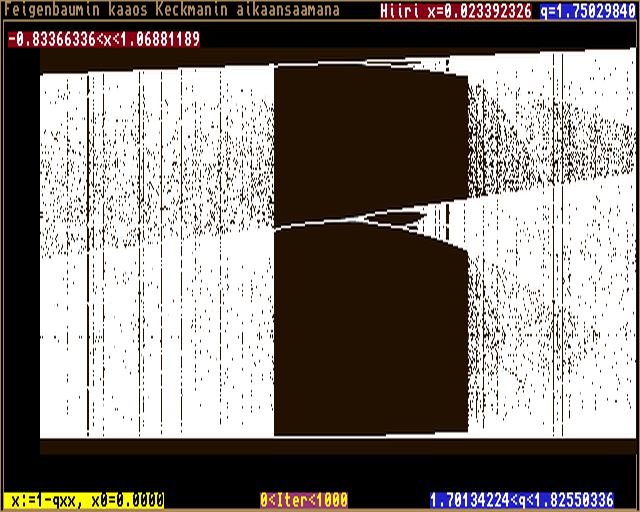
Aluetta 1.401:stä eteenpäin ei tunneta kovin tarkkaan. Mitään selkeätä matemaattista mallia ei ole sen käyttäytymiselle, vaikka selkeää säännönmukaisuutta sielläkin on havaittavissa. Determinismi ja matemaattinen tarkkuus antavat sijaa sattumalle ja kaaokselle. Tässä tuli lähinnä tutkittua vain q:ta, koska käsittääkseni yleensä alkuarvon x[0] valitseminen - ainakin kun pysytään alueella -1 < x[0] < 1, ei vaikuta raja-arvoon - poikkeuksena kiintopisteet. Lopuksi kuitenkin kuva siitä, miten käy kun alkuarvona onkin x[0]=-2 (alueella, jossa q lähestyy 0.75:sta). 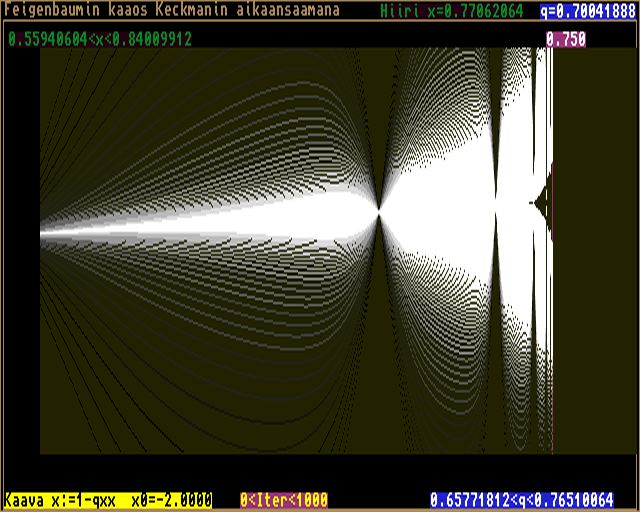
|